３．基本操作

3_3　基本操作その３（2019/11/16）

基本的なpandasの操作方法は、その２までで説明済みですが、ここでは、具体的なデータ分析の基本的な手順について説明します。但し、あくまで操作方法の説明が目的ですので、網羅的なデータ分析や更に深耕していくといった手順は考えていません。データに対する部分的な処理の説明になっています。
また、データ分析では、結果の理解を容易にするためにグラフ化は必須です。データ分析の手順に従って、グラフ化も併せて説明していきます。
ここまでできるようになれば、基礎編は終了です。一人でデータ分析ができるようになっていると思いますので、ご自分が持っているデータで試してみてください。
　

１）基本操作（その３）の実行

前にも述べましたが、本ブログでは、社会科学データの分析を主としています。データの種類は、以下の4種類です。
＜質的データ＞
　①名義尺度：単なる種類を示す尺度、性別（1:男、2：女）の様なデータ
　②順序尺度：順序に意味がある尺度、アンケート等のカテゴリー（1：悪い、2：普通、3：良い）の様なデータ
＜量的データ＞
　③間隔尺度：数値の間隔に意味のある尺度、気温や西暦（西暦0年に意味はない）の様なデータ
　④比例尺度：数値の比率にも意味のあるデータ、時間（2時間は、1時間の2倍長い）の様なデータ
　
データ分析は、「質的データ」、「量的データ」、「質的データと量的データ」の3種類に分けて説明していきます。
では、Warehouseの中の３．基本操作の「基本操作その３」をダウンロードして解凍したbasic3フォルダをc:\Python\basicの下に格納してください。basic3フォルダの中には、basic3.pyプログラムが格納されています。
IPythonを稼働させて、basic3.pyをエディタで開き、コメントを無視して、1行ずつ状況を確認しながら実行してみてください。エラーになる処理もあるので注意して実行してください。
尚、使用する入力データは、basic2の処理結果になります。

２）質的データ

ここでは、単にデータ分析の仕方についてだけを記載しますが、データ分析において最も重要なのは、データ分析の目的を明確にするという事です。目的を明確にし、仮説を立てて、データ分析でその確からしさを検証していくというのが通常のデータ分析の手順です。
ノーベル賞を取るような研究では、できることを全て試してみたり、色々と試している間に本来の目的とは異なる発見があるようなこともありますが、通常のデータ分析ではそのような進め方はしません。なぜなら、目的とそれを達成する為の期限があるからです。つまり、作戦を立てて行動することが必要だという事です。
さて、質的データの分析の話を進めます。質的データのカテゴリーは有限で、多くの場合、そのカテゴリー数は多くありません。多い場合は、階層化する等の工夫が必要です。そして、項目毎のカテゴリーが頭で容易に理解できるようになることが先決です。
例えば、動物のデータの比較をする場合、動物の種類は名義尺度で、質的データですが、比較しようとする動物の数が少ない場合は問題ありませが、多い場合は、ネコ科、イヌ科等にグループ化して比較できるようにします。
但し、都道府県別の犬と猫の数を比較する場合、47都道府県を地域別にグループ化しても良いですが、都道府県は、多くの人が理解が容易ですので北から順番に47個を並べるという事でも良いと思います。質的データの場合は、項目やカテゴリーを分かり易く並べるという事に注意してください。また、何を分からせたいのかに留意して比較するようにしてください。
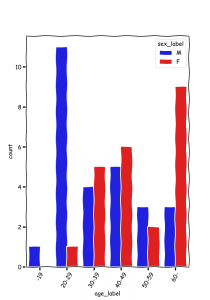
質的データの分析では、カテゴリー別の件数、割合、クロス集計、棒グラフ等が一般的に使用されます。
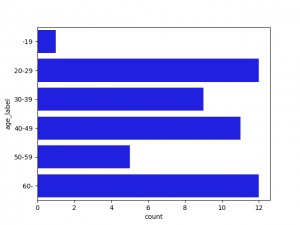
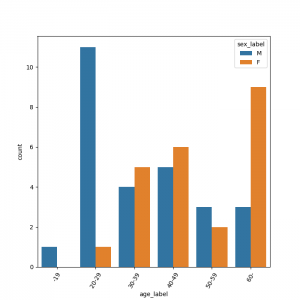
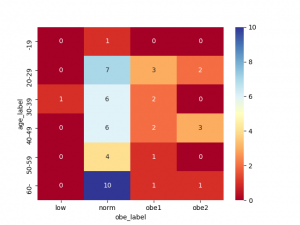
以下に、basic3.pyの棒グラフとクロス集計をグラフにしたヒートマップ図の事例を示します。
本ブログでは、seabornというグラフパッケージを中心に説明しますが、一部でmatplotlibというseabornの元となるグラフパッケージも活用しています。

３）量的データ

量的データは、実数データの集合という事になりますので、どの様に分布しているのかを掴む必要があります。実数データの基本統計量やヒストグラムによって分布状況を捉えます。
データ分析をする場合は、全ての変数に対して、先ずは、分布がどの様になっているのかを把握した上で分析を進めるようにしてください。
次に、変数間の関係性を分析します。一般的には、変数間の関係性を見る指標として相関係数をチェックします。多くの変数間の相関係数を一度に表示する相関行列で確認するのが一般的です。
但し、相関係数は関係性を示していますが、因果関係を示している訳ではなく、相関係数が高いからといって、その2つの変数が関係しあっているとはいえないことに注意してください。例えば、AとBの関係性が高いのは、AとBに直接的な関係が無く、AはCと関係が深く、BもCと関係が深いため、相関係数の数値だけ見るとAとBの関係性が高いように見えているだけかもしれませんし、もっと複雑な関係性があって、その様に見えているだけかもしれませんので注意してください。
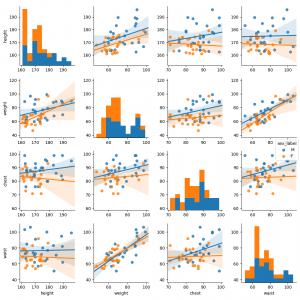
また、散布図を描くことで、その2つの変数間の関係性を目で見て確認することができます。seabornでは、散布図も相関行列の様に散布図行列として表現することができます。複数の散布図が、行列にマッピングされているというイメージです。一目で関係性を確認できる優れた機能です。
以下に、basic3.pyで作成したヒストグラム、散布図、散布図行列の事例を示します。

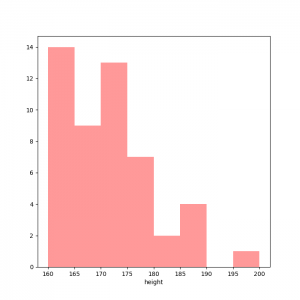
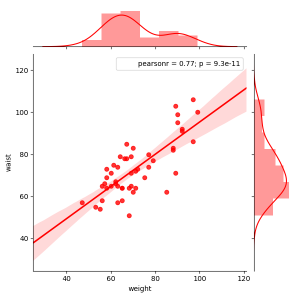
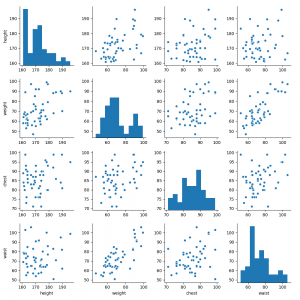
４）質的データと量的データ

多くの場合、分析対象のデータセットには、質的データと量的データが混在しています。データ分析の目的も、質的データの違いによって、量的データがどの様に影響されているかを探る場合が多いと思います。
もちろん、実際のデータ分析の目的はそのような単純なことではないかもしれませんが、目的を噛み砕いていくと個々にはそのような目的があることがあります。若しくは、目的を探るために、質的データと量的データの関係性を探るという事があります。
ここでは、質的データと量的データの関係性を示す一般的なグラフについて説明します。
データ処理としては、基本操作（その２）で示したgroupby等で質的データの組合せ毎の分析も行ってください。
データ分析は、組合せ毎の分析が最も重要です。しかし、全ての組合せを分析しようとすると時間がいくらあっても足りないということになります。先ずは、変数毎の状況を踏まえ、基本的な組合せの分析を行なった上で、方向性を見定めて詳細な分析へと深耕していくことになります。
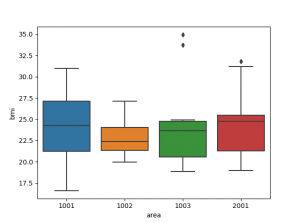
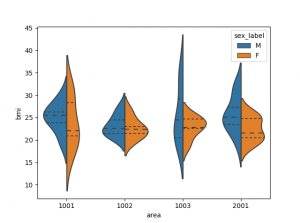
ここでは、性別のヒストグラムの比較、性別の散布図行列の比較、地域毎の箱ひげ図とバイオリン図による比較をしてみました。以下に事例を示します。

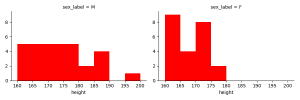
５）その他

Pythonでは、手書きの様なグラフを作成することも簡単にできます。Pythonのmatplotlibやseabornで描くすべてのグラフを手書き風にすることができます。
不真面目の様にとらわれることが無いのであれば、趣のある手書き風のグラフも良いかも知れません。
以下に、前述のヒストグラムを手書き風に変えた事例を示します。